Machine Learning: An Algorithmic Perspective 読んでいく(1)
機械学習に関する色んな書籍が世の中には出回っている。星の数ほどはないかもしれないけどかなりの数あると思う。
最近は「実装しながら説明していくよ!」という本も増えているそう。自分みたいなコーディングどへたくそな人間にとっては凄くありがたい(そして英語の勉強にもなる)。。そんな背景もあって以下の本を読むことになりました。

- 作者: Stephen Marsland
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 2014/11/17
- メディア: ハードカバー
- この商品を含むブログを見る
内容は
- chapter1: Intorduction
- chapter2: Preliminaries
- chapter3: Neurons, Neural Networks, and Linear Discriminants
- chapter4: The Multi-layer Perceptron
- chapter5: Radial Basis Functions and Splines
- chapter6: Dimensionality Reduction
- chapter7: Probabilistic Learning
- chapter8: Support Vector Machines
- chapter9: Optimisation and Search
- chapter10: Evolutionary Learning
- chapter11: Reinforcement Learning
- chapter12: Learning with Trees
- chapter13: Decision by Committee Ensemble Learning
- chapter14: Unsupervised Learning
- chapter15: Markov Chain Monte Carlo Methods
- chapter16: Graphical Models
- chapter17: Symmetric Weights and Deep Belief Networks
- chapter18: Gaussian Processes
と、かなり盛りだくさんである。全部読めばそれなりの知識が得られそうではあるが、さすがにしんどいのでまずは3,4章を読んでいく。
理論的な部分はかなり省略されており、入門用の本なのだと思う。あと完全に自分が頭の中を整理するためのものなので、読んでても参考にはなりません。。
3.1 The Brain and The Neuron
動物の脳を模倣したモデルを再現したら機械学習できるんじゃね?ってことで生まれた、パーセプトロンについての概要。脳内のニューロンを模したモデル。
脳内の化学物質(入力)によってニューロン内の電位が変動し、ある閾値を超えるとニューロンが発火する。その出力(発火するかしないか)がそのまま別のニューロンの入力となる。みたいな。
またニューロン同士のつながり(シナプス)には強さがある。Hebb's rule によると、発火しやすい二つのニューロンをつなぐシナプスは強固なものとなり、逆だとつながり弱くなる(最終的にはなくなる)。これによって他のニューロンへの入力を制御できる。
そこでMcCullonch と Pitts がニューロンを数学的にモデリングした。
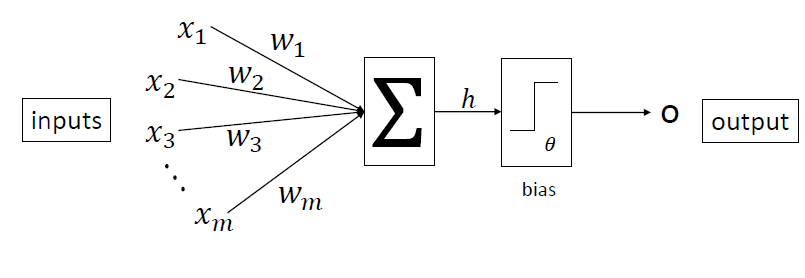
一つのニューロンへの入力hは、式で表すと以下のようになる
閾値はニューロンが発火するかしないかを決定するパラメータである。出力oは以下で決定する。
これは最も単純なモデルであるが、ちゃんと機能する。ただし実際のニューロンと異なる点も多々あるため留意する。例としては
- モデルは単一の出力しか返さないが、実際のニューロンの出力はパルス波の連続であり、それ自体が情報量を持つ。
- モデルの閾値はコンピュータのクロックごとに更新されるが、実際のニューロンは非同期的で(asynchronously)ランダムに更新される
さらに重み(シナプス)に関しても違いがある。シナプスには興奮性(excitatory)のものと抑制性(inhibitory)のものがあり、モデルの重みではこれらを正負で表している。さらにフィードバックの構造がなかったり...と色々違いはある。それらを改良したモデルも存在するが、現段階でも十分に興味深い結果が得られるとのこと。
ニューラルネットワークでは活性化関数を様々な非線形関数に変えて使用する。
3.2 Neural Networks
ある訓練データの特徴を学習し、未知のデータに対して、データやラベルを予測する。学習はニューロンの重みと閾値を変えることで行われる。
ここで問題となるのが、どのようにしてそれらのパラメータを更新するかである。
3.3 The Perceptron
ニューロンを並べて層を作ったのがパーセプトロン。
学習データとその目標値を与えることで、重みを更新していく。
閾値はニューロンごとに別々に設定するのは困難なので、入力項とまとめて考える。イメージは以下。

バイアスノードからは常に1または-1が入力され,重みを調整することで閾値を変えていく。
ここでは-1を入力とする。
重みの初期値は乱数で決定する。ここではとりあえず[-0.05, 0.05]くらいとする。
学習アルゴリズムは以下。
- Initialization
重みを小さい乱数で初期化
- Training
出力を計算
重み更新
- Recall
これを用いて、AND, OR, XORの二値分類を解いていく。
下の図のようなモデルを使い、実際に学習を行う。
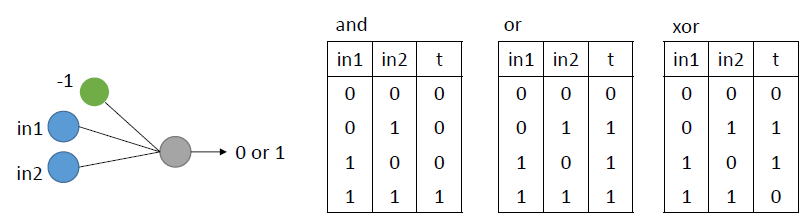
コードは以下の通り
#### pcn_logic_eg.py #### import numpy as np class pcn: """ A basic Perceptron """ def __init__(self,inputs,targets): """ Constructor """ # Set up network size if np.ndim(inputs)>1: self.nIn = np.shape(inputs)[1] else: self.nIn = 1 if np.ndim(targets)>1: self.nOut = np.shape(targets)[1] else: self.nOut = 1 self.nData = np.shape(inputs)[0] # Initialise network self.weights = np.random.rand(self.nIn+1,self.nOut)*0.1-0.05 def pcntrain(self,inputs,targets,eta,nIterations): """ Train the thing """ # Add the inputs that match the bias node inputs = np.concatenate((inputs,-np.ones((self.nData,1))),axis=1) # Training change = range(self.nData) for n in range(nIterations): self.activations = self.pcnfwd(inputs); self.weights -= eta*np.dot(np.transpose(inputs),self.activations-targets) print "Iteration: ", n print self.weights activations = self.pcnfwd(inputs) print "Final outputs are:" print activations #return self.weights def pcnfwd(self,inputs): """ Run the network forward """ # Compute activations activations = np.dot(inputs,self.weights) # Threshold the activations return np.where(activations>0,1,0) def confmat(self,inputs,targets): """Confusion matrix""" # Add the inputs that match the bias node inputs = np.concatenate((inputs,-np.ones((self.nData,1))),axis=1) outputs = np.dot(inputs,self.weights) nClasses = np.shape(targets)[1] if nClasses==1: nClasses = 2 outputs = np.where(outputs>0,1,0) else: # 1-of-N encoding outputs = np.argmax(outputs,1) targets = np.argmax(targets,1) cm = np.zeros((nClasses,nClasses)) for i in range(nClasses): for j in range(nClasses): cm[i,j] = np.sum(np.where(outputs==i,1,0)*np.where(targets==j,1,0)) print cm print np.trace(cm)/np.sum(cm)
#### logic.py #### import numpy as np inputs = np.array([[0,0,1],[0,1,0],[1,0,0],[1,1,0]]) # AND data ANDtargets = np.array([[0],[0],[0],[1]]) # OR data ORtargets = np.array([[0],[1],[1],[1]]) # XOR data XORtargets = np.array([[0],[1],[1],[0]]) import pcn_logic_eg print "AND logic function" pAND = pcn_logic_eg.pcn(inputs,ANDtargets) pAND.pcntrain(inputs,ANDtargets,0.25,6) print "OR logic function" pOR = pcn_logic_eg.pcn(inputs,ORtargets) pOR.pcntrain(inputs,ORtargets,0.25,6) print "XOR logic function" pXOR = pcn_logic_eg.pcn(inputs,XORtargets) pXOR.pcntrain(inputs,XORtargets,0.25,15)
実行結果↓

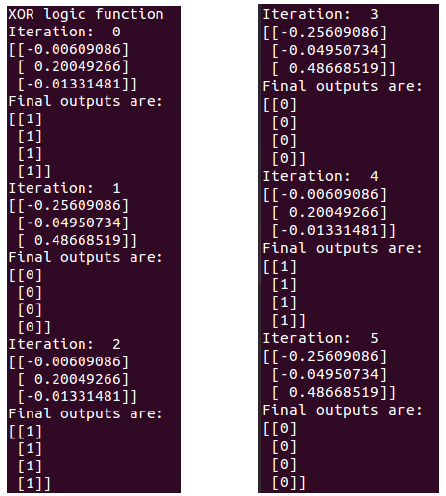
三つ出ている小数は,上から順にIn1, In2, biasの重みである。(biasの入力は常に-1であることに注意)
見てみると、ANDとORは正解に収束しているが,XORはうまく解けていないことがわかる。これはパーセプトロンが非線形問題を学習できないことによるものである。
ただし、少し工夫するとパーセプトロンでこの問題が解ける。
以下のように、入力を一つ増やしてやる。

XORの点を3次元に落としてやることで、線形関数でも分類ができるようになるわけである。
先ほどと同じコードを使ってやった結果↓

13iterationでXORが解けていることがわかる。
とりあえずここまで。