Machine Learning: An Algorithmic Perspective 読んでいく(3)
完全に忘れてたけど前回の続き。
読んでいるのはこれ

- 作者: Stephen Marsland
- 出版社/メーカー: Chapman and Hall/CRC
- 発売日: 2014/10/08
- メディア: Kindle版
- この商品を含むブログを見る
4.3 The Multi-Layer Perceptron in Practice
実際にMLPを使うときの注意点。
- hidden layer の数は学習データに依存
ネットワークの構造に正解はなく、データに依存する。理論的には層が多いほどモデルの表現能力があがり、どんな関数でも表現できるとされている。層の数を多くしなくても、hidden layer一層に多数のユニットを配置することでも同様の効果が得られる。ただし、使うメモリの量でいえばhidden layerを増やしたほうが、ユニット数を増やした場合より複雑なモデルが表現できるとされる研究事例もある。
- When to stop learning
MLPは学習を続けると過学習(over fitting)を起こし、テストデータに対して識別率が下がることが知られている。hidden layerを多くしたりユニットの数を増やすことで、ネットワークの表現能力が高くなると起こりやすい。
そこで学習する際に、validation dataset を用意してテストを行うことで、過学習を回避する方法がある。
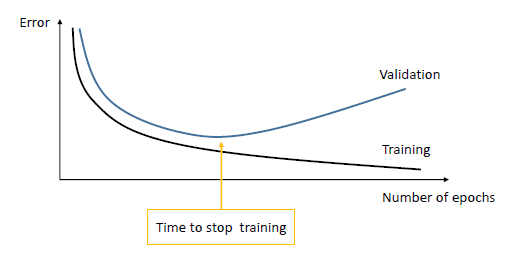
縦軸に誤差、横軸にエポック数をとった図をいかに示す。validation errorが上がり始める直前で学習を止めれば、過学習を防ぐことができる。
4.4 Deriving Back-Propagation
誤差逆伝搬法の計算について述べる。
式を書くのがめんどくさいので図で張り付ける。
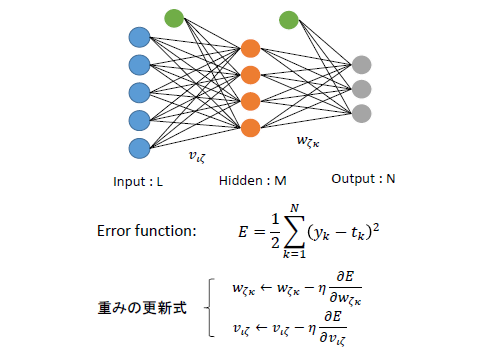
上手に示す三層ニューラルネットワークについて考える。
誤差関数は前回定義したのと同じ。1イテレーションごとに、誤差関数の負方向の勾配に学習率をかけた量だけ更新する。
まず、について考える。流れは以下のようになる。
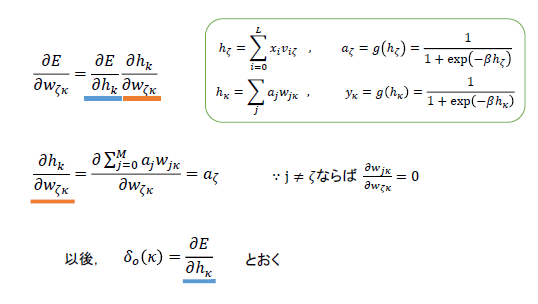
各層からのユニットの出力と重みの積の総和をとおく。またそれぞれに活性化関数を施したものを
と示す。
はMLP全体の出力である。活性化関数はロジスティックシグモイド関数とする。
誤差関数のの微分は、微分の連鎖法則で上のように書ける。
そのうち赤い下線を引いた項は、の場合のみ
となり、それ以外では0となるので、直ちに答えが求まる。ゆえに青い下線の項について考える。(以後、誤差関数
の
による微分を
とおく)
は以下のようにして求める。
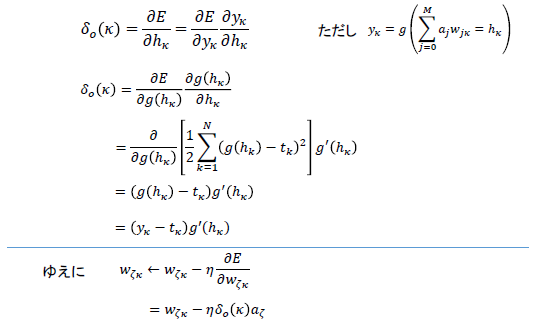
ここでも微分の連鎖法則を使う。
ロジスティックシグモイド関数の微分は
と求まるので、
の更新式は求まったことになる。
次にについて考える。流れは以下
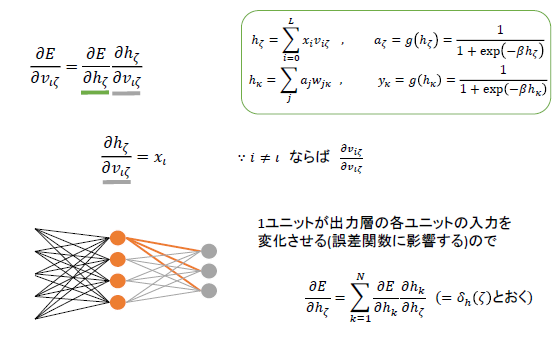
同じように微分の連鎖則を使う。グレーの下線の項については先ほどと同様にして直ちに求まる。
ただし緑の下線の項については注意する。図にもある通り、ユニット一つが出力層の各ユニットへ出力を返すので、中間層すべてのユニットの出力が誤差関数に影響する。ゆえに、は中間層の
について和をとる形となる。
は以下のようにする。
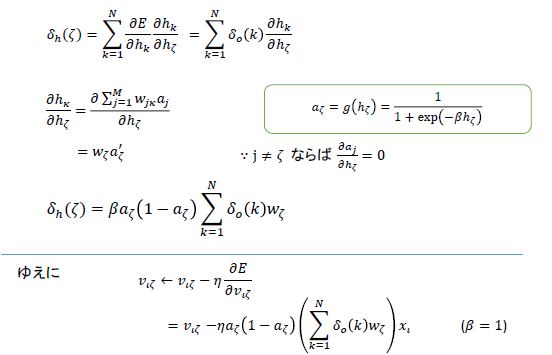
性懲りもなく連鎖則を使う。すると、を使って
が書けることがわかる。これはつまり前の層の誤差から次の層の誤差が求められるというわけである。このことから誤差逆伝搬法という名前がついている。
上の通りに計算すると、についても更新式が求まる。層が増えても、同様に計算していくことで誤差をすべての層に伝えることができる。
ただし層を増やしすぎた場合、入力層の近くまでくると誤差がうまく伝わらないことが発見され、それを機にニューラルネットの研究も一度下火になった。そこから今日のような盛り上がりを見せるとはだれが思ったであろうか。
MLPを実装した例が以下になる。ぶっちゃけ便利なライブラリがいろいろ開発されてるのでこれを使うことはまずないが、自分みたいな未熟者にはコードの勉強するいい機会なので一応。。
# mlp.py import numpy as np class mlp: """ A Multi-Layer Perceptron""" def __init__(self,inputs,targets,nhidden,beta=1,momentum=0.9,outtype='logistic'): """ Constructor """ # Set up network size self.nin = np.shape(inputs)[1] self.nout = np.shape(targets)[1] self.ndata = np.shape(inputs)[0] self.nhidden = nhidden self.beta = beta self.momentum = momentum self.outtype = outtype # Initialise network self.weights1 = (np.random.rand(self.nin+1,self.nhidden)-0.5)*2/np.sqrt(self.nin) self.weights2 = (np.random.rand(self.nhidden+1,self.nout)-0.5)*2/np.sqrt(self.nhidden) def earlystopping(self,inputs,targets,valid,validtargets,eta,niterations=100): valid = np.concatenate((valid,-np.ones((np.shape(valid)[0],1))),axis=1) old_val_error1 = 100002 old_val_error2 = 100001 new_val_error = 100000 count = 0 while (((old_val_error1 - new_val_error) > 0.001) or ((old_val_error2 - old_val_error1)>0.001)): count+=1 print count self.mlptrain(inputs,targets,eta,niterations) old_val_error2 = old_val_error1 old_val_error1 = new_val_error validout = self.mlpfwd(valid) new_val_error = 0.5*np.sum((validtargets-validout)**2) print "Stopped", new_val_error,old_val_error1, old_val_error2 return new_val_error def mlptrain(self,inputs,targets,eta,niterations): """ Train the thing """ # Add the inputs that match the bias node inputs = np.concatenate((inputs,-np.ones((self.ndata,1))),axis=1) change = range(self.ndata) updatew1 = np.zeros((np.shape(self.weights1))) updatew2 = np.zeros((np.shape(self.weights2))) for n in range(niterations): self.outputs = self.mlpfwd(inputs) error = 0.5*np.sum((self.outputs-targets)**2) if (np.mod(n,100)==0): print "Iteration: ",n, " Error: ",error # Different types of output neurons if self.outtype == 'linear': deltao = (self.outputs-targets)/self.ndata elif self.outtype == 'logistic': deltao = self.beta*(self.outputs-targets)*self.outputs*(1.0-self.outputs) elif self.outtype == 'softmax': deltao = (self.outputs-targets)*(self.outputs*(-self.outputs)+self.outputs)/self.ndata else: print "error" deltah = self.hidden*self.beta*(1.0-self.hidden)*(np.dot(deltao,np.transpose(self.weights2))) updatew1 = eta*(np.dot(np.transpose(inputs),deltah[:,:-1])) + self.momentum*updatew1 updatew2 = eta*(np.dot(np.transpose(self.hidden),deltao)) + self.momentum*updatew2 self.weights1 -= updatew1 self.weights2 -= updatew2 # Randomise order of inputs (not necessary for matrix-based calculation) #np.random.shuffle(change) #inputs = inputs[change,:] #targets = targets[change,:] def mlpfwd(self,inputs): """ Run the network forward """ self.hidden = np.dot(inputs,self.weights1); self.hidden = 1.0/(1.0+np.exp(-self.beta*self.hidden)) self.hidden = np.concatenate((self.hidden,-np.ones((np.shape(inputs)[0],1))),axis=1) outputs = np.dot(self.hidden,self.weights2); # Different types of output neurons if self.outtype == 'linear': return outputs elif self.outtype == 'logistic': return 1.0/(1.0+np.exp(-self.beta*outputs)) elif self.outtype == 'softmax': normalisers = np.sum(np.exp(outputs),axis=1)*np.ones((1,np.shape(outputs)[0])) return np.transpose(np.transpose(np.exp(outputs))/normalisers) else: print "error" def confmat(self,inputs,targets): """Confusion matrix""" # Add the inputs that match the bias node inputs = np.concatenate((inputs,-np.ones((np.shape(inputs)[0],1))),axis=1) outputs = self.mlpfwd(inputs) nclasses = np.shape(targets)[1] if nclasses==1: nclasses = 2 outputs = np.where(outputs>0.5,1,0) else: # 1-of-N encoding outputs = np.argmax(outputs,1) targets = np.argmax(targets,1) cm = np.zeros((nclasses,nclasses)) for i in range(nclasses): for j in range(nclasses): cm[i,j] = np.sum(np.where(outputs==i,1,0)*np.where(targets==j,1,0)) print "Confusion matrix is:" print cm print "Percentage Correct: ",np.trace(cm)/np.sum(cm)*100
これをand, xorについて試す。以下のコードで動かす。
# logic.py import numpy as np import mlp anddata = np.array([[0,0,0],[0,1,0],[1,0,0],[1,1,1]]) xordata = np.array([[0,0,0],[0,1,1],[1,0,1],[1,1,0]]) p = mlp.mlp(anddata[:,0:2],anddata[:,2:3],2) p.mlptrain(anddata[:,0:2],anddata[:,2:3],0.25,1001) p.confmat(anddata[:,0:2],anddata[:,2:3]) q = mlp.mlp(xordata[:,0:2],xordata[:,2:3],2,outtype='logistic') q.mlptrain(xordata[:,0:2],xordata[:,2:3],0.25,5001) q.confmat(xordata[:,0:2],xordata[:,2:3])
結果が以下↓
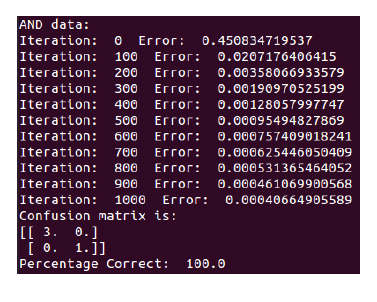
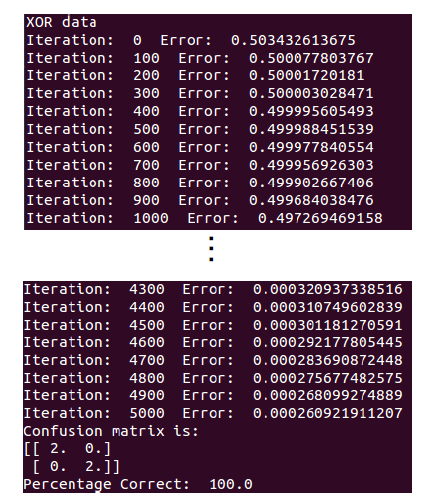
and, xorともに正しい答えが得られていることがわかる。ただしandについてはパーセプトロンよりも時間がかかっていることに注意。
とりあえずここまで。続きはまた読むかもしれない